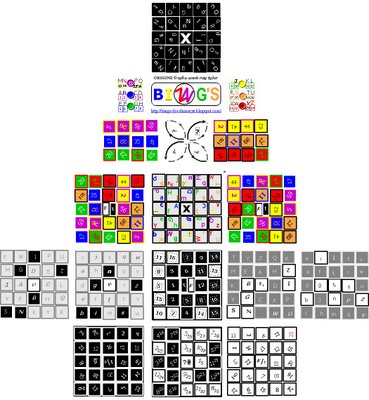
BINGO: under the ‘B’ five non-repeated values from the set 1-15; ‘I’ 16-30 ‘G’ 46-60 he ‘O’ 61-75 while under ‘N’ there are only 4 values out of 31-45 inclusive, since the central X has no value. The choice of 75 values may appear to be arbitrary, but not coincidental to the fact that a sum of numbers which total 75 are in fact of a particular mathematical significance. This ‘ideal average’ BINGO card has been divided into 4 geometric sets (blue, green,yellow,orange), and a split group of the 5th & 6th sets (violet & red), which Chess players may recognize as being the two symmetries of the Knight’s move [elL&Jay].The BINGO numbers are Nominal numbers, in effect ‘named’ or identified as 24 unique values out 75 possible, having no significance in themselves. Note that technically any number of multiple groupings of incremental (not necessarily sequential) values could be used. An argument could be made that the ordering of the files should correspond to the alphabetical sequence: hence BGINO as a little idea light goes on…there appears to be an interesting potential: B[O/X] ZINGS, also we might consider 4 points-of-view.

There are 24 counted numbers out of 75, each is a Cardinal value position. This nuance is readily understood within the context of ‘cardinal points’, the four principal directions, the compass ‘points’:North, East, South, and West. The Sub-Cardinal points are: North-East, North-West, South-West and South-East. Between the Cardinal and Sub-cardinal compass points are the Sub-Sub Cardinal points. Envision two symmetries (as if diagonals of squares equal to a circle’s diameter), the Clock-wise: North-north-east; East-south-east; South-south-west; West-north-west; and the Counter-clockwise points: North-north-west; West-south-west; South-south-east; East-north-east. Note that on the BINGO card, a 5x5 grid (tiling), there are 2 sets of Cardinal directions (blue & yellow) and 2 sets of Sub-Cardinal directions (green & orange) but that there are no ‘true’ Sub-sub Cardinal sets; the (Chess Knight) sets (violet & red) are 4.065 degrees ‘off’ from the 1/16 divisions of a circle. These Harmonics are the portal to ORIGINSZ © rt

The concept of ‘Ordinal’ or ‘ranking’ values of these cardinal value (nominals) is the critical feature which permits turning BINGO into an actual game/puzzle. Looking from the point-of-view convention of South to North the 5 random values from a choice of 15 in each successive column (from West to East) may be in either order – ascending, the conventional low to high, or descending. By defining them as the Tabular (like a table of values) ordinals, we can view them at the same time as being Functional (geometric positioned) ordinals corresponding to each of the six directional Cardinal groups in terms of their distance displacement from the center. To make this manageable a more practical adaptation of the alphabet, excluding O&X, i.e. 24 letters, (as in the Greek alphabet) is introduced in order to permit a further exploration of number which will lead us back to the properties employed to create Pachisi, (meaning 25), and subsequently Chaturanga (meaning quadripartite-division into four) the earliest known pre-cursor of Chess. In turn both can be related to the special case Nasik Magic Square and its geometric principle of recursion, the quantum leap from arithmetic to its geometric origins, and the corollary trigonometric and algebraic features, the elements which most likely led to the discovery of zero.

BI ZN GS © rt ( BOINGSZ, BINGZS, ZINGSBOX etc.) is the initial random scrambled BINGO card used to generate successive pairs of clones: through the simultaneous exchange between the Functional &Tabular ordinals. The determination of the scoring sequence[s] in this BINGO-for-dummY’s may be the world’s first play challenge for 2 to ‘n’ players where creative imagination, mathematical skill, and judicial risking of chance form the solution alternatives. It remains to discover if there are transferable real world applications related to finding the number of stages in its cycle: its binary extrapolation analogous to the tree root generation of ‘cellular automata’. Most intriguing as a game theme is to identify the patterns/sequences of the  Cardinal and Ordinal sets which sum to the same value - perfect solutions being equal to 75.

The key to this DUMMY is to recognize that the tabular ordering of successive columns (or files) is in terms of the functional (positional) ordering: the alpha ORDINALS, not the numbers themselves, whether the CARDINAL integers of a MAGIC SQUARE or any other structured array (even a random one!?) or the NOMINAL values in BINGO. (I used average values for ZINGSBOX puzzle). In effect this provides an insight to what was most likely the ‘origin’ of the gaming concept which was adopted to become the conventional ‘roulette on a grid’. The beautiful mathematics was probably not understood by the person or persons who introduced it – or it was ‘lost’ – all that survived was the one to one matching idea along ‘rows’ and diagonals (and other groupings).

This is the primer designed to become no less a popular pass-time and challenge than Sudoku, but unlike which is only the beginning of a voyage of discovery with extensions into Magic Squares, their recursion cycles, the connection to Chaturanga and the origin of Chess, all leading to the Master geometric model ORIGINSZ which I began developing in 1982.

Once upon a line, a point in time: a number, as a letter
marked its place in space,

but from its rigid viewpoint reached out to embrace a more universal reality.

As numbers come, so numbers go and some multiplied threefold

to stand like soldiers in a row doomed to become –BINGO –
why, and how did we fail

in our voyage of discovery where all is such perfect harmony?

But now let their inner truth be known and how magic springs:

BGINSZS… a child’s play game as the gateway to ORIGINSZ,

a geometric language by which to re-chart our mindscape

to challenge the twisted reason of this world

which cannot get its numbers straight

while its words are parsed to become absurd

as madmen plunder and destroy in their folly to claim God’s grace

The Divine Compass traces our ignoble fate:

Who will state Sum Ergo Cogito?

This puzzle is a (perfect) four points-of-view distribution, with a special 'universal' tiling of the average values used in BINGO (like in Bridge). From the standard position (of South looking North, columns East to West) what was the card of origin?
Hint: numerical values 1-24 are used for letters A-Z : where N=14 but skipping O, P=15, so that W=22 and skipping X, Y=23 Solution: Exchange functional alpha-numeric Ordinal values with their equivalent tabular values by substituting their corresponding Nominal(Cardinal) BINGO place value.

Test: ‘A F U N K Y’ Ordinals (of Cardinal Nominals) = 75 ; their Ordinal tabular (BINGO)Nominals = 228,
representing one quarter of their respective totals: 300 and 912 [950-38* center] average value of the “DUMMY”